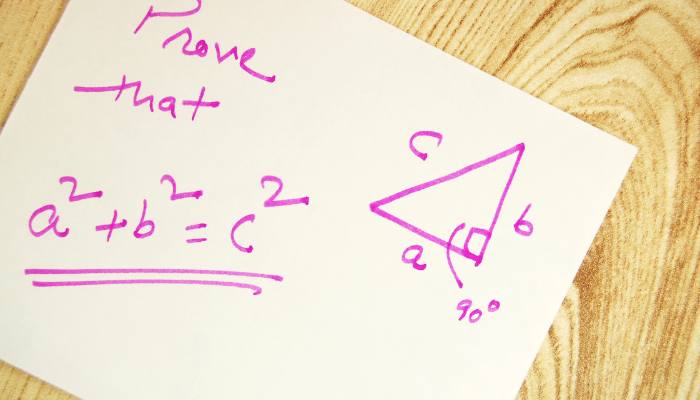Dalam matematika, terdapat suatu konsep yang sangat menarik yang dikenal sebagai “tripel Pythagoras.” Tripel Pythagoras adalah sebuah set bilangan bulat positif yang memenuhi persamaan Pythagoras, yang merupakan dasar dari teorema Pythagoras yang terkenal. Artikel ini akan mengulas lebih dalam tentang kelompok bilangan yang merupakan tripel Pythagoras.
Apa Itu Tripel Pythagoras?
Sebelum kita memahami apa itu kelompok bilangan yang merupakan tripel Pythagoras, mari kita terlebih dahulu memahami apa itu tripel Pythagoras itu sendiri. Tripel Pythagoras adalah set bilangan bulat positif a, b, dan c yang memenuhi persamaan Pythagoras:
a² + b² = c²
Di mana a, b, dan c adalah panjang sisi-sisi sebuah segitiga siku-siku. Dalam segitiga siku-siku, sisi dengan panjang c adalah hipotenusa, sedangkan sisi a dan b adalah kaki-kaki segitiga.
Kelompok Bilangan yang Memenuhi Persamaan Pythagoras
Sekarang, mari kita bahas tentang kelompok bilangan yang memenuhi persamaan Pythagoras. Kelompok bilangan ini sangat menarik karena dapat digunakan untuk menciptakan segitiga siku-siku yang berbeda. Ada beberapa kelompok bilangan yang merupakan tripel Pythagoras yang paling terkenal, yaitu:
1. Tripel Pythagoras Primitive
Tripel Pythagoras primitive adalah tripel Pythagoras yang memiliki angka-angka yang saling prima (tidak memiliki faktor persekutuan lebih dari 1). Contoh yang paling terkenal adalah (3, 4, 5) dan (5, 12, 13). Kelompok bilangan ini adalah dasar dari semua tripel Pythagoras.
2. Kelipatan Tripel Pythagoras
Tripel Pythagoras juga dapat diperoleh dengan mengalikan angka-angka dari tripel Pythagoras primitive dengan suatu bilangan bulat positif. Misalnya, jika kita mengalikan (3, 4, 5) dengan 2, kita akan mendapatkan tripel (6, 8, 10).
3. Tripel Pythagoras Khusus
Beberapa tripel Pythagoras memiliki sifat-sifat khusus. Misalnya, tripel (7, 24, 25) adalah tripel Pythagoras yang memiliki perbandingan sisi yang sama dengan tripel (3, 4, 5), hanya saja skala yang lebih besar.
Bagaimana Menggunakan Tripel Pythagoras?
Tripel Pythagoras memiliki banyak aplikasi dalam matematika dan dunia nyata. Salah satu yang paling terkenal adalah dalam perhitungan jarak, seperti dalam ilmu trigonometri. Tripel Pythagoras juga digunakan dalam teknik-teknik konstruksi dan pemodelan dalam ilmu fisika.
Contoh Soal
Yang termasuk tripel Pythagoras adalah kelompok i, iii, iv. Dalam pilihan iii dan iv yaitu pilihan B. Untuk menentukan apakah suatu kelompok termasuk tripel Pythagoras atau tidak, kita gunakan rumus Pythagoras. a² + b² = c², dengan c merupakan sisi terpanjang.
Penjelasan dengan langkah-langkah:
Diketahui:
Kelompok bilangan
i. 3, 4, 5
ii. 5, 13, 14
iii. 7, 24, 25
iv. 20, 21, 29
Ditanya:
Kelompok bilangan diatas yang merupakan tripel pythagoras.
Jawab:
Kita cek satu persatu.
i. 3, 4, 5
3² + 4² = 5²
9 + 16 = 25
25 = 25 (benar) artinya kelompok ini termasuk tripel Pythagoras.
ii. 5, 13, 14
5² + 13² = 14²
25 + 169 = 196
194 = 196 (salah) artinya kelompok ini tidak termasuk tripel Pythagoras.
iii. 7, 24, 25
7² + 24² = 25²
49 + 576 = 625
625 = 625 (benar) artinya kelompok ini termasuk tripel Pythagoras.
iv. 20, 21, 29
20² + 21² = 29²
400 + 441 = 841
841 = 841 (benar) artinya kelompok ini termasuk tripel Pythagoras.
Dengan demikian yang bukan termasuk tripel Pythagoras adalah kelompok ii. 5, 13, 14. dan yang termasuk tripel Pythagoras i, iii, iv.
Kesimpulan
Dalam artikel ini, kita telah membahas tentang kelompok bilangan yang merupakan tripel Pythagoras. Tripel Pythagoras adalah set bilangan bulat positif a, b, dan c yang memenuhi persamaan Pythagoras. Kelompok bilangan ini memiliki berbagai jenis, termasuk tripel Pythagoras primitive, kelipatan tripel Pythagoras, dan tripel Pythagoras khusus. Penggunaan tripel Pythagoras sangat beragam, dari perhitungan matematika hingga dunia nyata seperti konstruksi dan ilmu fisika.
Pertanyaan Umum (FAQ)
1. Apa itu tripel Pythagoras?
Tripel Pythagoras adalah set bilangan bulat positif a, b, dan c yang memenuhi persamaan Pythagoras, yaitu a² + b² = c².
2. Apa perbedaan antara tripel Pythagoras primitive dan kelipatan tripel Pythagoras?
Tripel Pythagoras primitive memiliki angka-angka yang saling prima, sedangkan kelipatan tripel Pythagoras diperoleh dengan mengalikan angka-angka dari tripel primitive dengan suatu bilangan bulat positif.
3. Apa contoh tripel Pythagoras khusus?
Contoh tripel Pythagoras khusus adalah (7, 24, 25), yang memiliki perbandingan sisi yang sama dengan tripel (3, 4, 5), hanya skala yang lebih besar.
4. Di mana tripel Pythagoras digunakan dalam kehidupan sehari-hari?
Tripel Pythagoras digunakan dalam perhitungan jarak, ilmu trigonometri, teknik konstruksi, dan pemodelan dalam ilmu fisika.
5. Apa manfaat utama dari memahami tripel Pythagoras?
Memahami tripel Pythagoras dapat membantu dalam memecahkan berbagai masalah matematika dan aplikasi dunia nyata yang melibatkan perhitungan jarak dan konstruksi geometri.